高校社会の倫理に登場する哲学者の思考法を学ぶシリーズです。
古代から哲学者と言われる人たちは、論理的思考によって本質について考えを深め、新しい発見をしてきました。
古代ギリシャの哲学者たちが残した哲学は、ルネサンスによって”再発見”されます。
17世紀以降、ヨーロッパの科学は他の地域よりも大きく発展していきます。その陰には哲学者たちの論理的思考がありました。
とくにイギリスを中心とした経験論と、ヨーロッパ大陸を中心とした合理論が大きな役割を果たしました。
この記事では、大陸合理論の祖と言われるルネ・デカルトが説いた、真理を発見するための四つの規則について解説します。
※経験論についてはイギリス経験論の祖ベーコンの記事があるので読んでみてください。
高校社会の倫理に登場する哲学者の思考法を学ぶシリーズです。 古代から哲学者と言われる人たちは、論理的思考によって本質について考えを深め、新しい発見をしてきました。 古代ギリシャの哲学者たちが残した哲学は、ルネサンスによって"再[…]
デカルト

ルネ・デカルト(1596年 – 1650年)は、フランス生まれの哲学者であり数学者です。
合理主義哲学の祖であり、近世哲学の祖とも言われています。「我思う、ゆえに我あり」という言葉を聞いたことがあるかもしれません。これはデカルトの哲学の命題です。
当時はスコラ哲学が主流でしたが、スコラ哲学は「信仰」による真理の獲得を目指していました。デカルトは「信仰」(神)ではなく人が持つ「理性」によって真理を探求していこうとしました。「信仰」(神)から解き放たれた思考を生み出したことこそデカルトが「近世哲学の祖」と言われている理由です。
数学者としてのデカルト
デカルトは高校の倫理の授業で登場しますが、デカルトが作ったものは中学の数学でも登場しています。

中学で習う比例反比例や関数のグラフは直交座標系と呼ばれていて、平面上の座標の概念を確立したデカルトの名前をとってデカルト座標系とも呼ばれています。
また、中学で習う数学の方程式は、わからない数字にXを置いて考えていますが、このXを置く方法で残っている一番古い書物はデカルトの著作です。
このように数学でも現在まで続く影響を与えているのがデカルトなのです。
デカルトの思考法
ここまでデカルトの数学者の実績を強調しましたが理由があります。デカルトの考え方の基本は演繹法というものだからです。演繹法とは私たちが習っている数学のように、普遍的なルール(公式)を前提にして、結論(答え)を出す思考法です。
数学を例に上げると「三角形の内角の合計は180°である」という普遍的なルールを前提として三角形の角度を求めますよね。
数学も演繹法も普遍的なルール(前提)が正しければ、答えは絶対的、必然的に正しくなるようになっています。
地球と太陽の距離のように、実際に長さを計測できなくても普遍的なルールをいくつも使うことでどのくらい離れているか計算できるのです。
演繹法は数学と相性が良く、デカルトは数学の研究によって得られた学びをもとに哲学を考えました。
反対にデカルトは普遍的なルールが成立しない歴史学などの人文学系の学問には興味を持ちませんでした。
演繹法の弱点
演繹法は普遍的なルール(前提)が正しければ、答えは絶対的、必然的に正しくなるという思考法です。
しかし演繹法にも弱点はあります。
- ルール(前提)が正しい必要がある
- 考えるのに時間がかかる
ルール(前提)が正しい必要がある
演繹法はルール(前提)が間違っていると、結論も間違ってしまいます。
「三角形の内角の合計は360°である」という前提で三角形の角度を求めようとすれば違う答えになってしまいますよね。
正しい前提が無ければ使えない思考法とも言えてしまうのです。
考えるのに時間がかかる
考えて結論を出すのに時間がかかります。数学の長ったらしい証明問題に苦戦したことはありませんか?
一つ一つのことを法則や定理などのルールを使って証明していきますよね。
しかも問題を見てストレートに答えまでたどり着くわけでもなく、あれでもないこれでもないとヒントを探しながら頑張って問題を解いた記憶があると思います。
演繹法は弱点を理解したうえで使いこなす必要があります。デカルトは弱点を回避する方法として四つの規則を編み出しました。
四つの規則
演繹法の弱点がわかっていれば、自分の抱えている問題の結論を絶対的、必然的に正しく導き出すことができます。
そこでデカルトは演繹法の弱点を回避する四つの規則を編み出しました。
四つの規則を使うことで、正しい前提しか使わない、四つを順番通りに進めれば迷わず結論にたどり着くことができます。
それが次の4つです。
- 明証
- 分析
- 総合
- 枚挙
「会社の利益を上げたい!」という場合にどのように使えばよいか具体例を上げつつ解説していきいます。
1.明証
「きちんと証明されたもの」で「自分も真実であると認めた」もの以外は前提に使わないことです。
定理や法則を自分で検証して証明してから考えるのは現実的ではありません。すでに証明されているものを使うようにしましょう。そして自分でもそのルール(前提)は正しいと信じられるもののみを使うことが重要です。
具体例
 社長
社長これでは神頼みになってしまってますよね。
「利益=売上-費用」のように利益を計算するには売上から費用を引いて計算します。このようにすでに使われている式を利用することで考えを進めることができます。
2.分析
考える問題をできるだけ細かく分けるようにします。
具体例
「利益=売上-費用」の式を基準に考えていきます。
 社長
社長式を見ると利益というのは売上から費用を引いたものだとわかります。
そして、利益を上げるには売上を上げるか費用を下げるかすればよいことがわかります。
 社長
社長売上がどのようにして計算されているか考えてみましょう。
例えば「売上=販売数×販売単価」 という式があります。
掛け算なので販売数を上げるか販売単価を上げることで売上は上がります。
 社長
社長販売数を上げたいなら、販売数がどのようにして計算されているか考えてみましょう。
「販売数=来店者数×購買率(買ってくれる割合)」 という式でさらに分けて考えればよいです。
 社長
社長このように何度も繰り返して課題を小さく分けるようにします。
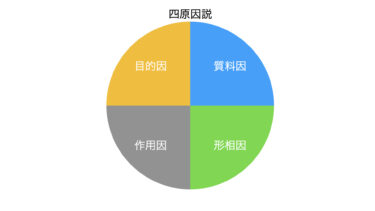
※他にも課題を分ける方法があります。アリストテレスの四原因説です。
高校社会の倫理に登場する哲学者の思考法を学ぶシリーズです。 古代から哲学者と言われる人たちは、論理的思考によって物事の本質について考えを深め、新しい考えを生み出してきました。 現代のビジネスの現場でも、様々な情報を組み合わせ、[…]
3.総合
大きな問題を細かく分けたら、一番簡単なものから順に解決していくことで大きな問題を解決できる道筋をつくります。
具体例
 社長
社長 社長
社長利益の要素を考えるときに一つずつ分解していきました。
- 利益=売上-費用
- 売上=販売数×販売単価
- 販売数=来店数×購買率
利益を1上げようと考えると、売上、費用、販売数、販売単価、来店数、購買率のどれを取り組めばよいかわかりづらいです。
しかし、来店数を1上げれば、計算式の答えである販売数が上がります。販売数が上がれば、売上も上がり、売上が上がれば利益も上がるよう芋づる式に利益まで上がる計算になります。
つまり来店数を上げれば、必然的にその上の式の数字も上がります。
このように、分解して一番細かくした要素から取り掛かれば良いのです。
4.枚挙
今までの工程で見落しがなかったか、全てを見直します。
具体例
 社長
社長 社長
社長見落としがあると数式上では利益が上がるハズでも下がってしまいます。
実は費用も次のような式で表すことができます。
費用=変動費+固定費
※変動費は売上によって変わる費用 固定費は売上にかかわらずかかる費用
変動費の例として、ラーメン屋さんならのラーメンの材料費などがこれに当たります。ラーメンを10杯売れば、材料費も10杯分かかりますよね。
なんでもかんでも節約してしまうと、売上によって変わる費用まで使わなくなってしまいます。
このように見落としがあるととんでもない間違いを犯してしまうのです。
このように四つの規則は現代でも活用する場面があります。(本来はもっと細かく分けます。業界によっては違う式を使ったりします。)
まとめ
デカルトは哲学者であり数学者でもありました。
数学者としても現代にまで影響があり、その思考法は演繹法と呼ばれるものでした。
演繹法は前提が正しければ、必然的、絶対的に正しい結論まで導くことができます。
しかし演繹法には2つ欠点があります。
- 前提が正しくないと結論を間違える
- 考える時間がかかる
この2つの弱点を克服するためにデカルトが編み出したのが四つの規則です。
四つの規則の順番で考えていくことでスムーズに演繹法を使えるようになります。
- 明証 証明されていて、自分も正しいと思える前提のみ使う
- 分析 問題をできるだけ細かく分ける
- 総合 一番簡単なものから順に解決していく
- 枚挙 明証、分析、総合で見落としが無かったか見直しする
4つの規則は現代でも当たり前のように使われています。